日本応用数理学会
2020年 研究部会連合発表会
プログラム
2020年2月6日
ご注意:本プログラムは暫定版であり変更される可能性があります.
3月4日
3月5日
▷ 科学技術計算と数値解析(1) [3月4日:09:30-10:50:Room A (6301)]
- 波動方程式と弾性方程式からなる連成系のシンプレクティッ ク性について / ○寺川 峻平 (神戸大学), 谷口 隆晴 (神戸大学) [概要]
ハミルトン系に対する数値計算手法としてはシンプレクティック法が有効であることが知られている.これは,シンプレクティック法がシンプレクティック形式を保つことに由来するが,複数の系からなる連成系については,どのような場合にシンプレクティック形式が保たれるのかが自明ではない.本研究では,複数のハミルトン系を相互作用により連成した場合に,シンプレクティック形式が保たれる条件について述べる.
- 時間方向対称性を利用した2つのエネルギー保存数値解法の等価条件について / ○石川 歩惟 (神戸大学), 谷口 隆晴 (神戸大学, JST さきがけ) [概要]
エネルギー保存則がラグランジアンの時間対称性から示されることを利用し,エネルギー保存性を離散化後にも保つスキームを設計する方法が,これまでにLagrange力学,Hamilton力学の場合それぞれで提案されている.しかし,得られるエネルギー保存スキーム同士が等価となる条件は未だ分かっていない.本講演では,Legendre変換に着目した両スキームの等価条件について述べる.
- 総質量保存則を持つGMSモデルに対する離散変分導関数法スキーム / ○奥村 真善美 (大阪大学情報科学研究科) [概要]
動的境界条件下でのCahn-Hilliard方程式系に対する構造保存スキームについて考察する。既に離散変分導関数法による、この問題に対する構造保存スキームの先行研究があるが、そのスキームは境界の外向き法線方向微分を前進差分で近似しており、また、その可解性の証明は得られていない。そこで、本研究ではその改良として、中心差分を用いて境界条件を近似した構造保存スキームを新たに構成し、その可解性を証明した。
- IMT型DE公式を用いた第2種Fredholm積分方程式の数値解法 / ○緒方 秀教 (電気通信大学大学院情報理工学研究科情報・ネットワーク工学専攻) [概要]
本講演では、1次元第2種Fredholm積分方程式に対し、IMT型DE数値積分公式を用いた数値解法を提案する。第2種Fredholm積分方程式に対しDE数値積分公式を用いて積分作用素を離散化した数値解法が提案されているが、この方法ではDE公式のメッシュ幅および積分標本点数という二つのパラメータを設定する必要があり、そのやり方は自明ではない。それに対し、IMT型DE公式を用いた本方法は積分標本点数ひとつだけを設定すればよく、パラメータ設定に迷う心配はない。そして、近似解の精度もDE公式による方法と遜色ない。講演ではいくつかの数値例を紹介して、本方法の有効性を示す。
▷ 科学技術計算と数値解析(2) [3月4日:13:30-14:50:Room A (6301)]
- カーネルを用いた補間における誤差指示関数の近似とその近似比 / ○大城 隆之介 (東京大学), 田中 健一郎 (東京大学) [概要]
関数補間手法の一つに再生核ヒルベルト空間のカーネルを用いた手法がある.
その手法の一つに Karvonen et al. (2019) による離散エネルギー最小化を利用するものがある.この手法中では誤差指示関数の近似を行うがその近似比は知られていない。
本研究では離散エネルギー最小化による手法における誤差指示関数の近似比について述べる。
- ピーク検出型数値複素積分と電子状態計算ソフトRSDFTへの応用 / ○星 健夫 (鳥取大), 小橋 恒士 (青山学院学), 吉見 一慶 (東大), 田中 健一郎 (東大) [概要]
電子状態計算ソフトRSDFTへの応用を主対象として,ピーク検出型計算に対する効率的な数値複素積分を提案する.電子状態計算など物理分野では,スペクトルにおいてピーク位置を求めることに大きな需要がある.通常は大規模エルミート行列固有値問題に帰着され,計算量の観点から困難になる.グリーン関数に効率的な複素数値積分を導入することで,新しい目的特定型の数値計算手法を提案する.計算コスト見積もりと理論的誤差解析を組み合わせることで,自動最適性のある計算ルーチンを構築する.
.
- Diracのデルタ関数を含む3次元境界値問題に対する有限要素解析 / ○中野 泰河 (新潟大学大学院自然科学研究科), 劉 雪峰 (新潟大学大学院自然科学研究科) [概要]
半導体分野の抵抗率測定法を支配する数学モデルの一つとしてDiracのデルタ関数を含む3次元境界値問題が考えられ,
当該問題に対する高精度な有限要素解析にはDiracのデルタ関数が持つ特異性の処理が不可欠である.
本講演では,Diracのデルタ関数を含む3次元境界値問題の有限要素解析において,
デルタ関数の特異点とメッシュの節点配置の関係によって生じた計算の不安定性と対応方法を紹介する.
- 摂動項を持つ静磁場問題に対するある Balancing Domain Decomposition 法の数値解析 / ○田上 大助 (九州大学 マス・フォア・インダストリ研究所) [概要]
Balancing Domain Decomposition (BDD) 法は, 大規模な計算モデルに対する高効率な並列計算手法である反復型領域分割法の前処理として知られている. 既に静弾性問題などでは BDD 法を用いた並列計算の有効性は示されているが, 静磁場問題では未だ並列計算の有効性は示されていない. 本講演では, 将来的な並列計算への高効率な適用を念頭に, 摂動項を持つ静磁場問題に対するある BDD 法の数値解析を紹介する.
▷ 科学技術計算と数値解析(3) [3月4日:15:00-16:20:Room A (6301)]
- 量子アルゴリズムの数値シミュレーションに必要な浮動小数点精度の再考 / ○齋藤 暁 (崇城大学情報学科) [概要]
典型的な量子コンピュータの計算過程を古典コンピュータ上で数値的にシミュレートする場合、必要なマシンイプシロンは量子回路幅に対して指数的に小さいはずであり、シミュレーションソフトウェアであるViamontesのQuIDDProや私のZKCM_QCでは多倍長精度演算を用いてきた。一方で、倍精度の浮動小数点演算のみでシミュレートしたという論文も散見される。シミュレーション手法とシミュレートする対象アルゴリズムごとに必要な計算精度を理論的および数値的に評価する。
- 非双曲型平衡点に対する局所Lyapunov関数の精度保証による構成 / ○中村 正男 (電気通信大学), 新田 光輝 (電気通信大学), 山本 野人 (電気通信大学) [概要]
局所Lyapunov関数の精度保証による構成は、連続力学系・離散力学系における双曲型平衡点・双曲型不動点の近傍で適用される手法が提案されている。本講演では、連続力学系における非双曲型平衡点の近傍でのLyapunov関数の構成について論じる。この話題に関しては、前年度の応用数理学会連合発表会において2次元の問題に限定して扱った。今回は、3次元以上への拡張について議論する。
- 微分代数の応用に向けた多項式常微分方程式モデルの簡約 / ○小松 瑞果 (神戸大学), 中岡 慎治 (北海道大学), 谷口 隆晴 (神戸大学) [概要]
微分代数とは,ある種の微分を演算に含むような代数的枠組みであり,計算アルゴリズムの停止性の問題から,その応用が限られていた.しかし,近年,場合によっては,計算アルゴリズムの停止性が保証されることが分かり,微分代数の応用の可能性が広がりつつある.以上を踏まえ,本研究では,微分代数の応用の可能性をさらに広げるために,多項式常微分方程式モデルの簡約を行う.
- Limit cycle through Van Der Pol equation in Homothermal Maintenance of Skunk Cabbage / ○Erdenebaatar Turtogtokh (Graduate School of Science and Engineering, Iwate University), Kawasaki Shuji (Graduate School of Science and Engineering, Iwate University), Ito Kikukatsu (Graduate School of Agriculture, Iwate University), Maruyama Koji (Graduate School of Science Osaka City University and Wolfram Research Asia Limited), Nugjgar Purevtsogt (Graduate school of Engineering and Applied Sciences, National University of Mongolia) [概要]
The plant called Skunk Cabbage is known to have a remarkable feature that it has a heating organ and retains its body temperature almost constant around 22~24 [°C] at the end of winter. As the mechanism of the homothermal maintenance, we have found that the control has a linear equilibrium phase and nonlinear nonequilibrium phase. In this study, we consider modeling the nonlinear behavior part, which is a report here applicability of the so-called Van der Pol equation as a possible candidate model, as well as we did attempt to determine whether the limit cycle behavior exists.
▷ 連続体力学の数理(1) [3月4日:09:30-10:50:Room B (6309)]
- ヘレ・ショウセル内の磁性流体の運動に対する基本解近似解法よるアプローチ / 榊原 航也 (京都大学/理化学研究所), 下地 優作 ((株) リンクアカデミー), ○矢崎 成俊 (明治大学) [概要]
本講演では,Hele-Shaw セル内の磁性流体に対する移動境界問題の数値計算の結果を報告する.
基本解近似解法ならびに適切な接線速度を導入することにより,体積保存条件を満たす数値計算スキームを導出し,磁性流体の時間発展に現れるスパイクパターンの定性的な挙動を理解することを目標とする.
- 構造の幾何学的非線形性を考慮した流体構造連成場の形状最適化 / ○片峯 英次 (岐阜工業高等専門学校), 河合 竜雅 (岐阜工業高等専門学校(学生)) [概要]
定常の流体構造連成場問題に対して,幾何学的非線形性を考慮した構造領域の剛性最大化を目的とする形状最適化問題を取り上げて,その解法を紹介する.問題を定式化し,随伴変数法を利用して形状修正の感度となる形状勾配密度関数を導出した.導出した感度に基づいて力法(あるいは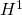 勾配法)を適用し,Freefem++を利用して解析した数値解析結果を紹介する.
勾配法)を適用し,Freefem++を利用して解析した数値解析結果を紹介する.
- 多孔質媒質中の乱流における渦粘性が初期値鋭敏性を示す条件 / ○鈴木 岳人 (青学大理工) [概要]
多孔質媒質中の乱流に対して、乱流エネルギーkとその散逸率εで状態を記述するk-εモデルを適用する。この時k-ε相空間上で一本の直線が共通のヌルクラインとなる。これにより定常状態での渦粘性が初期値に鋭敏に依存する場合としない場合が現れるが、その詳細な条件を議論する。
- 移流拡散方程式のための質量保存時間2次精度 Lagrange-Galerkin スキームとその2流体問題への応用 / ○野津 裕史 (金沢大学/JSTさきがけ), 二井 滉太 (金沢大学) [概要]
移流拡散問題のための質量保存型時間2次精度 Lagrange-Galerkin スキームを開発し、その誤差評価を行った。物質微分項の離散化は、特性曲線に沿った Adams-Bashforth 法に基づいている。また、これを2流体問題に適用し、2次元および3次元の数値シミュレーションを行った。これらの結果を報告する。
▷ 連続体力学の数理(2) [3月4日:11:00-12:20:Room B (6309)]
- Robin境界条件におけるBorn級数 / ○町田 学 (浜松医科大学), 中村 玄 (北海道大学) [概要]
拡散方程式に対するRobin境界条件においてBorn級数を考える。こうして、Neumann境界条件から出発して近似解を得ることができる。Born級数の収束と、数値実験について、得られた結果を報告する。
- 退化非線形放物型方程式と進行波 / ○市田 優 (明治大学大学院理工学研究科), 坂元 孝志 (明治大学理工学部) [概要]
本講演では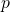 を自然数として,空間
を自然数として,空間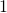 次元の退化非線形放物型方程式
次元の退化非線形放物型方程式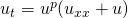 の進行波について考察する.この方程式は平面曲線の時間発展問題に由来する.我々は,ポアンカレ・コンパクト化の手法を応用することで,進行波解の存在とその漸近挙動について報告したい.
の進行波について考察する.この方程式は平面曲線の時間発展問題に由来する.我々は,ポアンカレ・コンパクト化の手法を応用することで,進行波解の存在とその漸近挙動について報告したい.
- [特別講演:40分]接触角条件付き面積保存型曲率流に対する進行波解の安定性について / ○可香谷 隆 (九州大学マス・フォア・インダストリ研究所) [概要]
本講演では,界面エネルギーの勾配流に対応する,面積保存型曲率流と呼ばれる曲線の運動方程式を扱う.ジョルダン閉曲線に対する上記の流れは,円に漸近する性質を持つが,接触角条件を課すことによって,進行波解が安定性を持つことを紹介する.この構造の違いは,エネルギー構造の変化に伴うものであり,関連しうる界面ダイナミクスについても触れる.
▷ 連続体力学の数理(3) [3月4日:13:30-14:50:Room B (6309)]
- 線型近似安定化トラクション項での抵抗境界条件による冠動脈血流シミュレーション / ○宇田 智紀 (東北大学材料科学高等研究所) [概要]
本研究の目的は,高解像度メッシュを用いた血流計算で患者固有の血栓症などの病理の数理的メカニズムの理解を進めることである.その課題が適正な流量実現と境界条件の設定である.抵抗境界条件は圧力流量比例を要請するが,不安定化要因となる.Bazilevsらの安定化トラクション項は非線型性のため大規模系での実装が難しい.そこで,前ステップの速度場を用いて線型近似した抵抗境界条件を試みたことをご報告する.
- 感染症流行の予防・治療限界モデル:ワクチン接種可能数と治療可能数を考慮して / ○祇園 大夢 (島根大学), 齋藤 保久 (島根大学), 矢崎 成俊 (明治大学) [概要]
感染症の予防と治療はその流行を抑制する役割として有効だが、ワクチン接種可能数や治療可能数(たとえば、病院の寝台数や薬量)には限りがある。本発表では、感染者集団を、治療不要な軽度感染者と治療を要する重度感染者に内分し、ワクチン接種可能数の限度とそれを超えて生じるワクチン非接種者の感染重度性、及び、重度感染者に施す治療可能数の限度を考慮した感染症流行モデルを提案し、それらの感染症流行への影響について論じる。
- 狭空間での弾性シートの破壊:座屈とき裂伸展の干渉効果 / ○増田 千紘 (横国環情), 工藤 大嗣 (横国環情), 松井 和己 (横国環情), 田中 良巳 (横国環情) [概要]
弾性シートの座屈を伴うき裂伸展挙動,とくに系を平行な2枚の剛体板の間の空間に閉じ込めて面外変形の大きさを拘束した場合の挙動を実験的に調べ,その結果をスケーリング解析をした.さらに,有限要素法による変形パターンの再現を行った結果についても報告する予定である.
- やわらかい固体のすべり摩擦における亜音速-超音速遷移:解析解との比較 / ○山口 哲生 (九大工), 家敷 拓弥 (九大工), 森田 健敬 (九大工), 澤江 義則 (九大工) [概要]
我々の実験研究によって,やわらかい弾性体であるゲルをその弾性波速度以上の速度ですべらせると,それ以下のときとはすべり挙動が全く異なることが分かっている.本研究では,定常状態における集中力と変形との関係であるGreen関数を求めることで,実験で用いた円筒-円筒接触における圧力分布を導くことに成功した.また,この圧力分布は,実験結果と概ね一致していることが分かった.さらに本研究では,定常状態の力学的安定性についても議論を行っている.講演では,これらの詳細を報告する予定である.
▷ 連続体力学の数理(4) [3月4日:15:00-16:20:Room B (6309)]
- 基本解の勾配を用いたsingular sources methodに関する一考察 / ○平井 椋介 (京都大学), 新納 和樹 (京都大学), 西村 直志 (京都大学) [概要]
逆散乱解析に対する数値解析手法の一つであるsingular sources methodにおいて,
基本解の勾配に基づくindicator functionを用いる方法について発表を行う.
特に基本解の勾配を用いることで,散乱体境界の近傍でindicator functionがよりはやく発散し,
indicator functionから散乱体境界の位置だけでなくその接線方向も求められることを示す.
- Comparative study of image segmentation methods based on a parametric approach(直接法による画像輪郭抽出法の比較研究) / ○Kolar Miroslav (チェコ工科大学/明治大学), 上形 泰英 (明治大学), 矢崎 成俊 (明治大学) [概要]
In this contribution, we study the qualitative behavior of different image segmentation approaches originating in the direct parametric description of moving curves. We assume the case of segmentation of a grayscale image by a single Jordan curve driven by different evolution laws enhanced by asymptotically uniform tangential redistribution of grid points.
(本講演では,曲線を動かす直接法によりいくつかの異なる画像輪郭抽出法を比較する.
その際,対象とする画像はグレースケールを仮定し,
分点の漸近的一様配置法を用いた接線速度と,
異なる法線方向の成長法則に従って時間発展する一つのジョルダン曲線によって画像の輪郭が抽出されるものとする.)
- 生体内の光伝播シミュレーションにおけるモンテカルロ法の検討 / ○山田 祐也 (京都大学情報学研究科), 川越 大輔 (京都大学情報学研究科), 藤原 宏志 (京都大学情報学研究科), 磯 祐介 (京都大学情報学研究科) [概要]
生体内の光学特性値決定に用いられるモンテカルロ法によるシミュレーションを実行するプログラムは多く公開されている。このため、複数のプログラムによる結果を定量的に比較検討することで、より信頼性の高いシミュレーション結果を得ることに寄与できると考えられる。従って、本講演では特によく用いられていると考えられるプログラムを利用して、シミュレーション結果を比較検討した結果を述べる。
- On reservoir computing with inertial form / ○本多 泰理 (東洋大学 情報連携学部) [概要]
Reservoir computing (RC)の一形態として、入力・中間層のユニット状態の時間発展がinertial manifoldを持つ形式を提案する。またその場合における、RCが満たすべき性質との関連、およびinertial manifold上での上記時間発展の解析方法について議論する。
▷ 応用可積分系(1) [3月4日:09:30-10:50:Room C (6310)]
- 完全グラフ上の離散
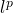 ソボレフ不等式の最良定数 / ○山岸 弘幸 (都立高専) [概要]
ソボレフ不等式の最良定数 / ○山岸 弘幸 (都立高専) [概要]
頂点数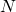 の完全グラフ
の完全グラフ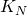 上での離散
上での離散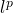 ソボレフ不等式の最良定数を求めた.
ソボレフ不等式の最良定数を求めた.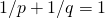 ,
,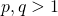 である.離散
である.離散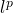 ソボレフ不等式はたわみの最大幅を,たわみの差分の
ソボレフ不等式はたわみの最大幅を,たわみの差分の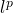 ノルムの定数倍で評価する不等式である.定数のうち,最も小さい定数が最良定数である.完全グラフの離散ラプラシアン行列
ノルムの定数倍で評価する不等式である.定数のうち,最も小さい定数が最良定数である.完全グラフの離散ラプラシアン行列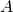 から一般化逆行列
から一般化逆行列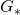 が導出できる.
が導出できる.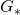 の任意の列ベクトルの差分の
の任意の列ベクトルの差分の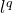 ノルムが最良定数となる.特に
ノルムが最良定数となる.特に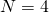 の場合は,正
の場合は,正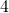 面体上でのたわみ問題となる.
面体上でのたわみ問題となる.
- C60フラーレン全異性体上の離散ソボレフ不等式の最良定数と最もかたいC60フラーレン / ○關戸 啓人 (京都大学), 亀高 惟倫 (大阪大学), 山岸 弘幸 (東京都立産業技術高等専門学校) [概要]
Cnフラーレンとは,炭素原子n個からなる球状の分子である.
各炭素原子が線形バネでつながっている古典力学モデルを考え,離散ソボレフ不等式の最良定数をフラーレンのかたさの指標とする.
本講演では,C60フラーレンの全1812個の異性体について,最良定数を求めることで,C60フラーレンの中で最もかたいフラーレンはバッキーボールであることを報告する.
- トポロジ型コンピュータワーム感染モデル / ○佐藤 大輔 (NTTネットワーク基盤技術研究所) [概要]
コンピュータワームにはスキャン型とトポロジ型があるが、トポロジ型の数理モデルはノード間の繋がりが複雑すぎて構築されていなかった。本発表では従来とは異なる視点での分類を行うことで数理モデル(リッカチ方程式)を導き、モデルが実データをよく表現していることを示した。またスキャン型での問題点の解決、可積分差分によってノード数有限の場合での全ノート感染の条件を導いた。
- 超離散可積分系による整数行列の単因子計算アルゴリズム / ○小林 克樹 (京都大学 情報学研究科) [概要]
超離散可積分系の(min, +)演算を(gcd, ×)演算に置き換えることで, 系に対応した形の整数行列の単因子が計算できることを示す.
本講演では特に超離散戸田方程式によって二重対角整数行列の単因子が計算できることを示す.
▷ 応用可積分系(2) [3月4日:11:00-12:20:Room C (6310)]
- 可積分系と美的形状の幾何 / ○梶原 健司 (九州大学マス・フォア・インダストリ研究所), Schief Wolfgang Karl (ニューサウスウェールズ大学), 井ノ口 順一 (筑波大学) [概要]
これまでの研究で,講演者らは車のデザイナーが美しいと感じる曲線から抽出された平面曲線の族「対数型美的曲線」(LAC)をを考察し,LACは相似幾何におけるオイラーの弾性曲線の類似物という特徴付けを得て,その空間曲線への一般化(空間LAC)を与えた.本講演では,その曲面への一般化として,空間LACが曲率線座標になっているような擬球曲面の相似幾何類似を提示する.
- Explicit expression for the curvature of an integrable discrete Euler’s elasticae and its application to shape identification / ○Graiff-Zurita Sebastian Elias (九州大学大学院数理学府), 鈴木 利友 (武庫川女子大学), 梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
Euler’s elasticae are curves obtained as critical points of the elastic energy. We will focus our attention to a known integrable discretization. In the first part, we will show that its discrete curvature can be expressed in terms of the Jacobi elliptic functions with the same functional shape as its continuous counterpart. This implies that the discrete Euler’s elastica can be seen as an interpolation of the continuous curve. In the second part, as an example of application, we will see how these curves can be used to characterize tiles of a wooden house built during the Meiji era.
- Spherical Kaleidocycles on 3-sphere / ○朴 炯基 (九州大学大学院数理学府), Rondomanski Jakub (ベルリン自由大学), Polthier Konrad (ベルリン自由大学), 梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
We consider rings of equivalent geodesic tetrahedra on 3-sphere, which is called the spherical Kaleidocycles. For the global rotation in the particular direction of spherical Kaleidocycles exhibits “turning over” motion via the stereographic projection. We present an algorithm to construct spherical Kaleidocycles and realize them by Javaview.
- 植物の根による水の吸収を考慮した土壌中の水浸透現象を表す定常モデル / ○田中 義久 (九州大学理学部), Triadis Dimetre (九州大学マス・フォア・インダストリ研究所/ラ・トローブ大学), 梶原 健司 (九州大学マス・フォア・インダストリ研究所) [概要]
植物の根による水の吸収を考慮した土壌の水浸透現象を記述するBroadbridgeモデルの定常状態を考察する。モデルは外力項付きBurgers方程式で記述され、Cole-Hopf変換と変数分離で変形ベッセル関数の微分方程式に帰着することに注目し、定常状態を記述する方程式を定式化する。モデルの制約と整合する定常解が存在する条件とそのときの最大総水量を求め、時間依存解の適切な初期条件、境界条件を示す。
▷ 応用可積分系(3) [3月4日:13:30-14:50:Room C (6310)]
- q値n近傍セルオートマトンのファジー化 / ○渡邉 扇之介 (小山工業高等専門学校), 西田 優樹 (同志社大学), 福田 亜希子 (芝浦工業大学), 渡邊 芳英 (同志社大学) [概要]
2値3近傍セルオートマトン(ECA)に対し,ブール表現由来の多項式表現を利用することで{0,1}の2値ではなく,[0,1]の実数値をとれるように拡張したCAをファジーセルオートマトン(FCA)という.一般のq値n近傍CAを従来の発想でファジー化しようとすると元の離散値の独立性が失われてしまう.本講演では,一般のq値n近傍CAに対して元の離散値の独立性を保持した新しいファジー化の方法を提案する.
- 3値3近傍ファジーセルオートマトンの保存則 / ○西田 優樹 (同志社大学), 渡邉 扇之介 (小山工業高等専門学校), 福田 亜希子 (芝浦工業大学), 渡邊 芳英 (同志社大学) [概要]
q値n近傍セルオートマトン(CA)は,セルのとる値をq次元ベクトルで表現することでファジー化できる。本講演では,周期境界条件をみたす3値3近傍ファジーCAに対して,一周期にわたる成分の総和が時間発展で保存されるルールの列挙を行う。この保存則は,3値3近傍CAにおいてある値をとるセルの数が不変であることの拡張になっている。本講演で提案する手法は,他の加法的保存量やq値n近傍CAにも適用可能である。
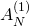 型ミューテーションの線形化 / ○野邊 厚 (千葉大学), 松木平 淳太 (龍谷大学) [概要]
型ミューテーションの線形化 / ○野邊 厚 (千葉大学), 松木平 淳太 (龍谷大学) [概要]
ランク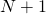 のクラスター代数の
のクラスター代数の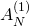 型ミューテーションから導かれる双有理写像力学系は、
型ミューテーションから導かれる双有理写像力学系は、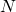 個の独立な保存量をもつ離散可積分系である。本講演では、保存量を用いて双有理写像力学系を線形化し、一般解を求める。
個の独立な保存量をもつ離散可積分系である。本講演では、保存量を用いて双有理写像力学系を線形化し、一般解を求める。
- 有理型Heun作用素とWilson双直交関数について / ○辻本 諭 (京都大学情報学研究科), Vinet Luc (Montreal大学数学研究センター), Zhedanov Alexei (中国人民大学情報学部) [概要]
変数 x の n 次多項式と m 次多項式をそれぞれ分子分母とする有理関数を [n/m] 型有理関数とよぶ.[(n-1)/n] 型の有理関数を [n/(n+1)] 型有理関数にうつす最も一般的な2階差分作用素として有理型Heun作用素を導入し,Ruijsenaars-van Diejen Hamiltonianの竹村による特殊化との関係について議論する.さらに,その古典類似からWilson双直交関数系が得られることを示す.
▷ 応用可積分系(4) [3月4日:15:00-16:20:Room C (6310)]
- 符号付き超離散系におけるリミットサイクルの対応物の構成 / ○鈴木 清一朗 (法政大学大学院理工学研究科システム理工学専攻経営システム系), 礒島 伸 (法政大学理工学部経営システム工学科) [概要]
リミットサイクルをもつことで知られる、ファン・デル・ポール方程式の符号付き超離散類似を構成する。複数の初期値問題の解を分類して状態遷移図にまとめ、周期解やリミットサイクルの存在を議論し、また、差分方程式の解との関係についても議論する。
▷ 行列・固有値問題の解法とその応用(1) [3月4日:11:00-12:20:Room D (6317)]
- エルミート行列レゾルベントの二次形式に対するシフト付きランチョス法 / ○保國 惠一 (筑波大学) [概要]
ランチョス法が与える縮減行列によりエルミート行列レゾルベントの二次形式を計算することを考える。ヤコビ行列レゾルベントの(1, 1)成分はランチョス法に8回の演算を追加すると計算でき、シフト付きランチョス法は反復回数の2倍の数のモーメントを一致させて対象とする二次形式を近似すること、及び本手法が破綻することなく解を与える条件を示す。従来法と比較した提案法の有効性を数値実験で示す。
- Global Krylov部分空間法に対する相互作用型残差スムージング / ○相原 研輔 (東京都市大学) [概要]
短い漸化式を用いるKrylov部分空間法では,残差ノルムの振動により丸め誤差が拡大し,偽収束が起きる.この問題を改善するため,最近,相互作用型残差スムージングが提案された.これは,スムージング前後の反復列が丸め誤差の影響を抑えるように相互作用する新しい平滑化スキームである.本発表では,この手法を行列方程式などに有効なGlobal Krylov部分空間法にも適用できるよう拡張し,その有効性を数値実験により示す.
- 非線形力学系のためのKrylov部分空間法 / ○橋本 悠香 (NTT / 慶大), 野寺 隆 (慶大) [概要]
時系列データ解析の手法のひとつとして,データが非線形力学系から生じたと考え,力学系の時間発展を表す作用素,Perron-Frobenius作用素を推定する方法が注目を集めている.Perron-Frobenius作用素は,Hilbert空間上の線形作用素として定義されるため,これを推定するためのKrylov部分空間法が利用できる.しかし,上記問題にKrylov部分空間法を適用する場合,最終的に得たい近似が古典的な問題設定におけるものとは異なる場合がある.本研究は,非線形力学系にKrylov部分空間法を適用した際の解析を行い,その意味について述べる.
- Arnoldi型反復を用いたblock SS-CAA法の改良 / ○今倉 暁 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
一般化固有値問題および非線形固有値問題に対する有力な超並列固有値解法として、複素モーメント型固有値解法が知られている.これらの解法は、固有対精度を改善するために、反復計算と組み合わせて用いられる.本研究では,block Arnoldi法に基づく複素モーメント型固有値解法であるblock SS-CAA法の収束性改善を目的とし、Arnoldi型反復を適用する新しい手法を提案する.また、誤差解析および数値実験から提案法の有効性を示す.
▷ 行列・固有値問題の解法とその応用(2) [3月4日:13:30-14:50:Room D (6317)]
- [招待講演:40分] 行列理論からみた最小作用の原理について / ○鷲尾 巧 ((株)UT-Heart研究所) [概要]
最小作用の原理では、力学系の運動は作用積分を最小にするような軌道に沿って実現されると主張する。この最小という言葉使いは誤解を招きやすく、例えば調和振動子の場合には時間範囲を半周期よりも大きくとると運動方程式が与える軌道は作用積分の極値となるものの最小ではないことが行列の固有値理論から容易に示せる。本講演では、作用積分を時間方向に離散化し空間座標に対するテーラー展開を適用した際に生じる二次形式の固有値分布を解析することにより、作用積分の不定値性が古典力学的軌道や量子力学におけるファインマン経路積分など物理に及ぼす影響について考察する。
- ノイズを含むデータに対し概収束を保証する動的モード分解の計算手法 / ○相島 健助 (法政大学) [概要]
動的モード分解は高次元時系列データに対する有力な解析手法であり,様々な観点から精力的に研究が行われている.動的モード分解の計算には特異値分解がよく用いられるが,データが確率的なノイズを含む場合の理論解析は少なく,収束性を議論する数学的枠組み自体が曖昧なのが現状である.本発表では,動的モード分解の背景となるKoopman作用素の性質に着目したノイズの統計モデルを与え,概収束を保証する動的モード分解の一般的な計算手法を示す.
- 少数の実数シフトのレゾルベントで構成されたフィルタによる実対称定値一般固有値問題の下端固有対の解法について / ○村上 弘 (首都大学東京) [概要]
実対称定値一般固有値問題の近似固有対を求めるためのフィルタとして,少数のレゾルベントの線形結合の作用のチェビシェフ多項式であるものを採用する.レゾルベントのシフトに複素数を用いる場合の定式化は,十分に良いものが既に得られている.しかしレゾルベントのシフトに実数だけを用いる場合の良い定式化は,問題を固有値が下端にある近似固有対を求める場合に限定しても,まだ得られていないので,それについて考察を行う.
▷ 行列・固有値問題の解法とその応用(3) [3月4日:15:00-16:20:Room D (6317)]
- [招待講演:40分] Computing intervals containing matrix fractional powers / ○宮島 信也 (岩手大学) [概要]
Two numerical algorithms are proposed for computing interval matrices containing the matrix fractional powers. These algorithms are based on verified block diagonalization (VBD) recently rediscovered by the author. The first algorithm uses the VBD based on a numerical spectral decomposition, and involves only cubic complexity under an assumption. The second algorithm adopts the VBD based on a numerical Jordan decomposition, and is applicable even for defective matrices.
- 行列指数関数に対する数値的検証法の改良 / ○中村 圭汰 (岩手大学), 宮島 信也 (岩手大学) [概要]
行列指数関数の関数値に対する数値的検証法がMiyajimaにより提案されている。この方法ではψ_1関数と呼ばれる(スカラー)関数の関数値を包含する区間が計算される。この計算において区間の半径が増大する事例が発見された。この増大は最終的に得られる行列指数関数値を包含する区間の半径の増大を引き起こす。本講演ではψ_1関数値を包含する区間の計算方法を改良することにより、Miyajimaの方法よりも一般に小さな半径を与える方法を提案する。
- 行列のすべての固有値に対するロバストな数値的検証法 / ○今 貴一 (岩手大学), 宮島 信也 (岩手大学) [概要]
行列のすべての固有値に対する数値的検証法については、いくつかの方法が知られている。これらの方法は行列の次元の3乗に比例する演算回数で実行可能な一方、数値計算により得られた固有ベクトルから構成される行列が悪条件である場合に破綻する。本講演では、数値計算によるシュール分解と対角行列による相似変換を利用することにより、行列の次元の3乗に比例する演算回数で実行可能かつ上記の行列が悪条件でも破綻しない方法を提案する。
▷ 行列・固有値問題の解法とその応用(4) [3月4日:16:30-17:50:Room D (6317)]
- Convergence analysis of inner-iteration preconditioned GMRES method for least squares problems / ○LIAO ZEYU (The Graduate University for Advanced Studies, SOKENDAI), HAYAMI KEN (The Graduate University for Advanced Studies, SOKENDAI, and NII) [概要]
We will explain the super-linear convergence of the inner-iteration preconditioned GMRES method for least squares problems, by considering the effect of clustered eigenvalues of the preconditioned coefficient matrix. We show that the theoretically predicted convergence behavior matches numerical experiment results.
- 特異対称系に対するGMRES法とRRGMRES法の数値実験による収束解析 / ○杉原 光太 (国立情報学研究所), 速水 謙 (国立情報学研究所 総合研究大学院大学) [概要]
辺要素有限要素法を用いた電磁場解析等で生じる特異対称系において,右辺が係数行列の値域に属さない場合と属する場合について,丸め誤差に強いGMRES法とRange Restricted GMRES (RRGMRES)法の収束性を数値実験により比較する.
まず,右辺が値域に属さない場合,GMRES法よりRRGMRES法の方が収束が良い系があることを示し,原因を論じる.次に,GMRES法の残差ノルムが右辺の値域に属さない成分のノルムに収束しない原因を論じる.
最後に,右辺が値域に属する場合についても,両手法の収束性を比較する.
- 特異な大規模疎行列の4倍精度演算を用いたLU分解 / ○鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]
複合材料による弾性体方程式や半導体問題のドリフト拡散方程式の離散化で得られる大規模疎行列の条件数は非常に大きくなることが知られている. 並列計算向けの手法であるFETI領域分割法では部分領域の人工境界にNeumannデータを与えるため, 部分剛性行列は特異になる. 行列の核の空間がFETI反復法の構成に重要であるが, 条件数が大きい場合はLU分解の過程で浮動小数点演算による擾乱のため, 行列のランクの数値的な決定が難しくなる. 行列に対するスケーリング前処理と4倍精度演算の活用により DOI:10.1002/nme.4729 で提案したアルゴリズムの適用範囲を拡大できることを示す.
▷ 数理政治学 [3月4日:11:00-12:20:Room E (6318)]
- コンフリクト解決のためのグラフモデル(GMCR)による国際問題分析および拡張概念の提案 / ○加藤 有紀子 (東京工業大学) [概要]
国際関係における対立について、ゲーム理論から派生した枠組みの一つである『コンフリクト解決のためのグラフモデル ( GMCR :The Graph Model for Conflict Resolution)』の枠組みを用いて分析を行う。さらに、国際問題の分析を通して得られた洞察を活かし、GMCRの標準的な分析方法からの発展形としての新しい拡張概念を提案する。
- 衆参両院の選挙区配分議席を併せた公平性の分析 / ○諸星 穂積 (政策研究大学院大学) [概要]
衆議院と参議院の選挙ではどちらも並立制を採用しており,共に都道府県を単位とした議席の配分を行う制度をもっている.各県には衆参それぞれの議席が配分されているが,それを統合的に扱って,公平性がどのくらい実現しているのかを過去のデータから算出してみた結果を報告する.併せて定数配分の代表的な方法を用いた場合のシミュレーション結果についても報告する.
- 得票率(VS)と議席占有率(SS)の関係に関する計量分析の経緯-三乗則と存続可能性関数の応用 / ○大山 達雄 (政策研究大学院大学), 小林 和博 (青山学院大学) [概要]
選挙結果分析の代表的課題としての得票率(VS)と議席占有率(SS)の関係については、1960年に英国選挙データを基にM.G.KendalとA.Stuartによる論文の中で、三乗則が提起されて以来、それらの一般化、拡張に基づく理論的成果をもとに多くの研究結果が得られ、実証分析が行われている。本発表では筆者らがネットワークシステムの頑健性評価手法として提起した存続可能性関数に基づく理論構築と応用、実証分析結果、特に得票率(VS)と議席占有率(SS)の関係における三乗則との関係を中心に紹介する。
▷ 数論アルゴリズムとその応用(1) [3月4日:13:30-14:50:Room E (6318)]
- グレブナー基底計算における多項式選択について / ○新田 篤志 (首都大学東京大学院・修士課程二年), 星 雄大 (首都大学東京大学院・修士課程一年), 伊藤 琢真 (情報通信研究機構・研究員), 篠原 直行 (情報通信研究機構・主任研究員), 内山 成憲 (首都大学東京・教授) [概要]
グレブナー基底計算には Buchberger algorithm や F4 など様々なアルゴリズムが知られており, それらに対する改良も多く提案されている. これらのアルゴリズムの効率は, 使用する項順序, 不要な S 多項式の削除, 多項式の計算順序などと関係があることが知られている. このうち多項式の計算順序については詳細に言及されることが少なく, 未知の部分も多い項目である. 本講演では Buchberger algorithm 内での操作のうち, S 多項式生成に必要な多項式の組の選択, reducer の選択を対象に最適化を検証し、数値実験を実施した結果について述べ, その考察を与える.
- 2次強Frobeniusテストを用いた素数判定法について / ○原田 悠汰 (首都大学東京大学院修士課程2年), 伊丹 洸陽 (首都大学東京大学院修士課程1年), 篠原 直行 (情報通信研究機構主任研究員), 内山 成憲 (首都大学東京教授) [概要]
一般的によく用いられている確率的素数判定テストとしてMiller-Rabin テストがある.このテストに関して,底を小さい素数から順に動かしたとき,連続してテストを通過する最小の合成数を探索することにより,条件付きの効率的な確定的素数判定アルゴリズムを実現できる.本発表では,Miller-Rabinテストよりも判定効率のよい素数判定法として知られている2次強Frobeniusテストを用いて同様な実験を行い,その結果に関する考察を述べる.
- Edwards曲線を用いた3者間SIDHについて / 内山 成憲 (首都大学東京・教授), ○深見 心 (首都大学東京大学院修士課程2年) [概要]
同種写像暗号SIDHは耐量子計算機暗号の候補の一つであり、超特異楕円曲線間の同種写像計算問題の困難性に安全性の根拠をおく暗号方式である。SIDHは、通常Montgomery曲線を用いて実装することにより、演算や同種写像計算の高速化を実現している。一方最近、KimらによってEdwards曲線上での同種写像計算が示され、Montgomery曲線とEdwards曲線を用いた手法でSIDHの高速実装を行った。本講演では、彼らが用いた手法を3者間でのSIDHに適応し、その結果について述べる。
- 超特異楕円曲線上の同種写像グラフにおけるサイクルについて / ○小貫 啓史 (東京大学大学院情報理工学系研究科), 相川 勇輔 (三菱電機株式会社), 高木 剛 (東京大学大学院情報理工学系研究科) [概要]
本発表では, 耐量子暗号の1つであるSIKEにおける同種写像グラフのサイクルについて考察する. 我々は, そのグラフの頂点の1つの曲線の自己準同型環の構造を特定し, サイクルがあるDiophantus方程式の解と対応することを示した. そして, SIKEの具体的なパラメータであるSIKEp434とSIKEp503において, その方程式の解を求めることで同種写像グラフのサイクルを全て求めた.
▷ 数論アルゴリズムとその応用(2) [3月4日:15:00-16:20:Room E (6318)]
- 約数関数σ(n)とオイラー関数φ(n)を含む不定方程式の整数解について / 寺井 伸浩 (大分大学理工学部), ○新庄 慶基 (大分大学大学院工学研究科博士後期課程工学専攻環境工学コース), 仲敷 沙耶 (大分大学工学部知能情報システム工学科) [概要]
本講演は、nを正の整数とし、約数関数σ(n)とオイラー関数φ(n)を含む不定方程式σ(n)±φ(n)=p^x(p:素数)について考え、それらの正の整数解について研究を行った。ここで、x=1である正の整数解は無数に存在するので、x>1の場合について考える。特に、p=3のとき、n=q^kとした不定方程式σ(q^k )±φ(q^k )=3^xの場合で様々な結果が得られたのでそれらについて紹介する。本研究には初等的方法を用いて証明を行い、得られた正の整数解は数式処理システムMAGMAを用いて確かめる。
- 一般化3x+1予想の平均サイクル長と、整数環の特徴量との相関について / ○藤井 大輔 (名古屋大学大学院 多元数理科学研究科) [概要]
3x+1予想(Collatz予想)は「整数上の変換fを f(x)=x/2 (if x is even) or 3x+1 (if x is odd) と定めたとき、任意の正整数xについて、ある正整数kが存在しf^k(x)=1 である」と定式化される。このとき数列a_n=f^n(1) は(1,4,2)なるサイクル(循環節)をもつという。講演者は3x+1予想を代数体の整数環に拡張した問題について、捕捉可能なサイクルの長さが整数環の特徴量(単数群,イデアル類群)を反映していると推測できる数値計算の観察結果を得たのでこれを報告する。
- 有限体を用いた数独解の構成 / ○桑嶋 大地 (東邦大学大学院), 足立 智子 (東邦大学) [概要]
数独解は、数独パズルの空白のセルを全て数字で埋めた完成形である。
数独解は、ラテン方陣と密接な関係がある。
位数nのラテン方陣とは、n×nの配列に、n個の文字(シンボルと呼ぶ)を各行および各列のシンボルが全て異なるように並べた配列である。
シンボルの集合が有限体の時に、数独解がどのように構成できるかを述べる。
▷ ウェーブレット(1) [3月4日:13:30-14:50:Room F (6325)]
- [特別講演:40分] Hardy空間H^2(R)上のウェーブレットの構成とその性質 / ○橋本 紘史 (筑波大学), 木下 保 (筑波大学) [概要]
Hardy空間H^2(R)は上半平面上の古典的Hardy空間の実軸への極限によって実現される. また, H^2(R)は正の周波数しか含まない点で信号処理においても重要である. 本講演ではH^2(R)における正規直交ウェーブレットをMRAの視点から構成し, その無限遠での減衰評価を得たことを紹介する.
- [特別講演:40分] 新しい正規直交ウェーブレット基底とそれを用いたヒルベルト変換ペアの構築 / ○戸田 浩 (豊橋技術科学大学), 章 忠 (豊橋技術科学大学) [概要]
最近,筆者らは新しい正規直交ウェーブレット基底を発見した.この基底は,従来の正規直交ウェーブレット基底にはない特徴を持つ.また必要に応じて,任意のダイレーションや異なるダイレーションの混在等,様々な条件の基に設計でき,その基底関数は様々な形状に設計することが出来る.これらの新しい正規直交ウェーブレット基底を基礎に,様々なヒルベルト変換ペアを構築する.
▷ ウェーブレット(2) [3月4日:15:00-16:20:Room F (6325)]
- [特別講演:40分] ウェーブレット解析の40-Hz聴性定常反応への適用 / ○井川 信子 (流通経済大学), 守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学) [概要]
ヒトの耳に音刺激を与えてられる脳波である聴性誘発脳波には、
聴性脳幹反応と聴性定常反応がある。聴性脳幹反応波形を生成する
誘発脳波の加算過程にウェーブレット解析を適用して得られた結果から、
発生機序由来を含む40-Hz聴性定常反応のウェーブレット解析の適用に
ついて議論する。
- Parseval frame が満たす不等式について / ○萬代 武史 (大阪電気通信大学) [概要]
Parseval frame の特徴づけと関連した性質について整理し,Parseval frame が満たすある不等式について報告する.これは,各ベクトルの間の内積や距離と,各ベクトルの大きさとの間の関係を表す不等式であり,粗く言うと「大きさが1に近いベクトルは他のベクトルから離れている」ということを意味する.
▷ Quality of Computations (1)(10:10〜) [3月5日:10:10-10:50:Room A (6301)]
- 片側急減衰関数の全無限積分に対する鶴田らのSE公式の理論誤差評価の改善 / ○野村 友暉 (広島市立大学), 岡山 友昭 (広島市立大学) [概要]
t→±∞で急減衰する解析的な関数f(t)の全無限積分は,打ち切った複合台形則で非常に高精度に近似できることが知られている.ただし,f(t)がt→∞では急減衰でもt→-∞では急減衰でない場合も考えられる.この場合に対し,変数変換によって被積分関数を急減衰関数にした上で複合台形則を適用する方法が提案され,また見積もりが可能な誤差評価も鶴田らによって与えられている.本研究ではその誤差評価の改善を行った.
- 片側急減衰関数に対するSE-Sinc関数近似の改善と理論誤差評価 / ○白石 朋也 (広島市立大学), 岡山 友昭 (広島市立大学) [概要]
t→±∞で急減衰する解析的な関数f(t)は,Sinc関数近似によって非常に高精度に近似できることが知られている.ただし,f(t)がt→∞では急減衰でもt→-∞では急減衰でない場合も考えられる.この場合に対し,変数変換によって関数を急減衰関数にした上でSinc関数近似を適用する方法がStengerによって提案されている.本研究では変数変換の改善と誤差の見積もりが可能な誤差評価を行った.
▷ Quality of Computations (2) [3月5日:11:00-12:20:Room A (6301)]
- 単精度演算が高速なGPUを用いた行列積のエラーフリー変換 / ○尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学), 椋木 大地 (理研R-CCS) [概要]
本講演では,単精度浮動小数点演算が倍精度浮動小数点演算よりも超高速な数値計算環境における行列積のエラーフリー変換について述べる.入力の行列が倍精度浮動小数点数で与えられる場合において,高速な単精度演算を活用したエラーフリー変換を提案する.一部のGPUでは単精度演算が倍精度演算に比べて10倍以上高速であり,このような数値計算環境において提案手法の有効性を示す.
- 大規模密行列に対する固有値問題の精度保証法 / ○寺尾 剛史 (芝浦工業大学), 尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
我々は、固有値問題に対する全固有値の精度保証付き数値計算法を提案した。この手法は、先行研究の保証法で用いられる誤差解析の上限を改良したものである。また、提案手法を用いて実対称行列の標準固有値と一般化固有値、エルミート行列に対する標準固有値に対する精度保証法をスーパーコンピュータ上で実装した。本発表では、大規模並列計算機上でのスケーラビリティと精度に関する数値実験結果を紹介する。
- Banach 空間における有界線形作用素の近似に対する収束性 / ○木下 武彦 (九大情基セ), 渡部 善隆 (九大情基セ), 中尾 充宏 (早大理工) [概要]
本講演では有界線形作用素に対するある近似作用素を定義し,その収束性を考察する.
この近似作用素は妥当な仮定の下で対象となる有界線形作用素に強収束する事を報告する.
さらに,近似作用素の作用素ノルムは対象となる有界線形作用素の作用素ノルムに収束する事も分かった.
- 曲線の位置関係判定に関わる厳密計算法 / ○邵 文炳 (中国科学技術大学・新潟大学(D1)), 劉 雪峰 (新潟大学), 陳 発来 (中国科学技術大学) [概要]
A robust and efficient algorithm based on subdivision algorithm and the Newton-Kantorovich theorem is proposed for finding the intersection of algebraic curve within a specified area. The main feature our proposed algorithm is that the position of the computed intersection points is guaranteed. In the implementation of this algorithm, the Bernstein-Bézier representation and resultant method are used to efficiently judge the distribution of curve intersection in the specified region, and the Newton-Kantorovich theorem is used to calculate the verified intersection points. The algorithm is efficient measured in running times.
Got it, thanks!Looks good to me.Thanks!
▷ Quality of Computations (3) [3月5日:13:30-14:50:Room A (6301)]
- Smallest Singular Value of Asymptotic Diagonally Dominant Matrix and Delay Differential Equation / ○Shin’ichi Oishi (Waseda University) [概要]
A definition of an asymptotic diagonally dominant matrix is given for a complex square matrix. Theorems are given for estimating a lower bound for the smallest singular value of an asymptotic diagonally dominant matrix. An extension is shown for a block asymptotic diagonally dominant matrix. Several examples are presented. Especially, a main theorem is shown to be useful in a verified numerical inclusion of a periodic solution for a nonlinear delay differential equation modeling El Niño phenomena.
- Rigorous integration of smooth vector fields around spiral saddles with an application to the cubic Chua’s attractor / ○Warwick Tucker (Uppsala University), Zbigniew Galias (AGH-University of Science and Technology) [概要]
We present a general mathematical framework for integrating smooth vector fields in the vicinity of a fixed point with a spiral saddle.
We restrict our study to the three-dimensional setting, where the stable manifold is of spiral type (and thus two-dimensional), and the unstable manifold is one-dimensional.
As an application, we apply our work to a concrete situation: the cubic Chua’s equations.
Here, we present a computer assisted proof of the existence of a trapping region for the flow.
- Nonlinear transformations for interval methods of global optimization / ○Tibor Csendes (University of Szeged), Elvira D. Antal (University of Szeged) [概要]
With the advent of symbolic computer algebra systems the possibility has become clear for reforming the optimization problems into a more advantageous form.
The advantages of such simplifications are many-folded.
At one hand the respective functions can hopefully be evaluated with less operations.
Then we can recognize such redundant relations among the variables, that usually cannot be noticed.
Knowing these allows us to determine the subspace that consists only of optimal points.
And finally, due to the possible dimension decrease the iteration numbers of most of the optimization techniques can drop.
The procedure does not require human interaction, hence large scale and complex problems can become solvable by applying our simplification tool.
The present paper overviews our work done on this field, and new results are demonstrated on the application of the novel algorithm to improve the efficiency and precision of interval arithmetic based optimization algorithms.
- A computer assisted proof of the Jones conjecture / ○Jonathan Jaquette (Brandeis University) [概要]
A classical example of a nonlinear delay differential equations is Wright’s equation:
y'(t) = − α y(t − 1)[1 + y(t)], considering α > 0 and y(t) > −1.
This talk discusses two conjectures associated with this equation:
Wright’s conjecture (1955), which states that the origin is the global attractor for all α ∈ (0, π/2];
and Jones’ conjecture (1962), which states that there is a unique slowly oscillating periodic solution for α > π/2.
In this talk, I will discuss our computer assisted proofs of these conjectures.
To prove Wright’s conjecture our approach relies on a careful investigation of the neighborhood of the Hopf bifurcation occurring at α = π/2.
Using a rigorous numerical integrator we characterize slowly oscillating periodic solutions and calculate their stability, proving Jones conjecture for α ∈ [1.9, 6.0] and thereby all α ≥ 1.9.
We complete the proof of Jones conjecture using global optimization methods, extended to treat infinite dimensional problems.
▷ Quality of Computations (4) [3月5日:15:00-16:20:Room A (6301)]
- A priori error estimates for Poisson’s equation with discontinuous coefficients / ○Kazuaki Tanaka (Waseda University), Mitsuhiro T. Nakao (Waseda University) [概要]
We provide an explicit a priori error estimate for Poisson’s equation with discontinuous coefficients.
The proposed estimates can be applied to Galerkin approximations.
Application to finite element approximations is demonstrated.
- Preconditioning of Taylor models, implementation and test cases / ○Florian Bünger (Hamburg university of technology) [概要]
Makino and Berz introduced the Taylor model approach for validated integration of initial value problems (IVPs) for ordinary differential equations (ODEs).
Especially, they invented preconditioning of Taylor models for stabilizing the integration and proposed the following different types:
parallelepiped preconditioning (with and without blunting), QR preconditioning, and curvilinear preconditioning.
We review these types of preconditioning and show how they are implemented in INTLAB’s verified ODE solver verifyode by stating explicit MATLAB code. Finally, we test our implementation with several examples.
- Interval Linear Systems – Beyond the Krawczyk Operato / ○Marko Lange (Hamburg university of technology) [概要]
The Krawczyk operator was introduced in the late ’60s for solving interval non-linear systems.
For a long time the Krawczyk operator was considered state of the art also for verified solutions of linear systems with or without interval uncertainties.
More recently, semi direct methods that first validate and then exploit the H-property of the preconditioned system matrix are replacing the Krawczyk operator in many interval toolboxes.
This is motivated by the increased efficiency of these methods rather than an improved quality.
In this talk we will show that the interval Jacobi operator yields at least as good results as the Krawczyk operator and also competes with the more recent semi direct methods introduced by Rump and Minamihata.
Moreover, we introduce a new method for solving interval linear systems based on the magnitude method introduced by Hladik.
- TBA / ○TBA [概要]
▷ 応用カオス(1)・乱数の生成と評価セッション [3月5日:09:30-10:50:Room B (6309)]
- 量子乱数生成による量子ビットの統計的評価 / ○田村 賢太郎 (慶應義塾大学), レイモンド・ ルディー (IBM東京基礎研究所), 鹿野 豊 (慶應義塾大学) [概要]
量子力学では物理量の測定結果が確率的であるため, 理想的な量子コンピュータは真の乱数生成器となる. 一方, 実際の量子コンピュータではノイズ等の影響で, 出力乱数に偏り・規則性・相関が生じることが考えられる. 本研究では, IBMの量子コンピュータに内蔵されている量子ビットで乱数を生成し, 乱数列から量子ビットの偏りや量子ビット間の相関を定量的に評価した.
- P値の分布とのKolmogorov-Smirnov検定を用いた乱数性判定へのカオス真軌道の応用 / ○山口 明宏 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学) [概要]
乱数検定における乱数性の判定指標の一つとして,検定で得られたP値の分布と一様分布との適合度検定が用いられているが,P値の分布の離散性が判定結果に影響することが複数の研究で示されている.本研究では,判定結果へのP値の分布の離散性の影響の低減を目的として,対象とする擬似乱数系列と理想的な乱数と統計的に同等な系列を生成できるカオス真軌道を用いた擬似乱数系列との2標本Kolmogorov-Smirnov検定を提案し,参照分布を一様分布,P値の厳密分布,カオス真軌道によって得られるP値の経験分布とした場合について検定を行った結果を報告する.
- 置換多項式を用いたブロック暗号の乱数性評価 / ○中安 慶輔 (京都大学), 岩崎 淳 (京都大学), 梅野 健 (京都大学) [概要]
高速・軽量なブロック暗号の開発を目的として、置換多項式を組み込んだ一般化Feistel構造の暗号を提案する。提案手法は軽量暗号とされるCLEFIAよりも高速であり、NIST乱数検定ツールを用いた安全性評価に合格する。
- Maurerユニバーサル統計検定における参照分布形状の導出 / ○岩崎 淳 (京都大学) [概要]
NIST SP800-22に含まれているMaurerユニバーサル統計検定の参照分布は正規分布であることが仮定されている.本発表では,乱数長を無限大にする極限で参照分布が何らかの意味で正規分布に収束することを示す.
▷ 応用カオス(2) [3月5日:11:00-12:20:Room B (6309)]
- カオス尺度の拡張によるローレンツ系のカオスの定量化 / ○井上 啓 (山陽小野田市立山口東京理科大学工学部), 真尾 朋行 (東芝情報システム株式会社・京都大学大学院情報学研究科), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学大学院情報学研究科) [概要]
エントロピー型カオス尺度(以下,カオス尺度と略)は情報理論の観点から導入されたカオスを定量化する指標である。著者等は、拡張されたカオス尺度(以下、拡張型カオス尺度と略)の極限が、ある典型的な条件の下で全リアプノフ指数の総和と一致することを既に示した。なお、拡張型カオス尺度は時系列のみから計算可能であるため、著者等は多次元系の時系列データのカオスの定量化を目指している。本発表では、多次元系の典型的なカオスモデルであるローレンツ系を取り上げ、極限を取らない状況で拡張型カオス尺度とリアプノフ指数との比較を行う。
- 身体負荷および精神負荷と心拍変動のカオス性との関連について / ○真尾 朋行 (京都大学/東芝情報システム株式会社), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学) [概要]
生体データ等の分析において,データのカオス性に着目した分析法としてカオス尺度を用いることを検討している.カオス尺度は,カオスを定量化する指標として提案されており,近年,カオス尺度とリアプノフ指数との関連が明らかになってきている.
本発表では,被験者に身体負荷および精神負荷を加えて心拍間隔(RRI)を計測する実験を行い,それぞれの状態における,心拍変動解析に基づく自律神経活動指標とカオス尺度が示す傾向について報告・考察する.
- 共振条件と無線電力伝送との関係性の評価 / ○本山 雅孝 (京都大学大学院情報学研究科数理工学専攻), 梅野 健 (京都大学大学院情報学研究科数理工学専攻) [概要]
現在無線電力伝送の実用化に向けて実験を行っていますが、コイル間距離を同軸上で伸ばして
限界離隔距離まで行った際に、軸を垂直方向にずらした結果どのように伝送電力が変化するのか
調査したので結果を報告する。
- 特性関数を用いた価格変動の相関およびランダムウォーク仮説の検証 / 梅野 健 (京都大学), ○椎橋 広貴 (京都大学) [概要]
金融商品の価格変動はランダムウォークに従うといわれているが,実際には短い期間においては直前の変動による影響を受けて変化している.本研究では価格変動が安定分布に従うという仮定のもと,ランダムウォークのモデルをARモデルにて作成し,実際の金の価格変動のデータと比較して,データの自己相関の有無を検証する.自己相関は特性関数を用いて計算する方法を提案し,特性関数のパラメータ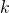 と,時系列のラグ
と,時系列のラグ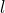 で捉えられる自己相関関数により,金融市場モデルの一つのパラダイムである効率的市場仮説,すなわちランダムウォーク仮説が実データで成立するかを検証する.
で捉えられる自己相関関数により,金融市場モデルの一つのパラダイムである効率的市場仮説,すなわちランダムウォーク仮説が実データで成立するかを検証する.
▷ 応用カオス(3) [3月5日:13:30-14:50:Room B (6309)]
- 結合可解カオス系の同期現象と同期条件について / ○比果 奨人 (京都大学), 梅野 健 (京都大学) [概要]
初期値が微量でも違えば、同じ決定論的法則にしたがって生成されたとしても、全く異なる不規則な軌道を描く初期値に鋭敏な性質を持つカオス系に対し、二つの系に、相互にある重みをつけた結合を行い観察すると、(つまり、相互に一定の影響を与え続けるカオスモデルを考えた)その重みに関する、ある条件下でその両方の軌道が全く同じ値をとりながら数値変動し、また、ある条件下で、不変の関係式(等式)を保って数値変動する同期現象が確認できた。本論では、その同期現象が起こる重みの条件を条件付きリアプノフ指数により導出し、シミュレーション結果との整合性を調べた。
- ある2次元保測Anosov写像におけるPerron-Frobenius作用素の固有関数について / ○吉田 賢典 (首都大理), 吉野 元 (首都大理), 首藤 啓 (首都大理), Lippolis Domenico (江蘇大理) [概要]
Perron-Frobenius作用素における絶対値が1より小さい固有値の中で最大のものを第二固有値と呼ぶ。もし、第二固有値が孤立していれば、その固有関数は系の緩和過程に対して最も支配的であることが期待される。本講演では、非線形摂動が加えられたArnoldの猫写像におけるPerron-Frobenius作用素が孤立した第二固有値を持つこと、および、その固有関数が系の不安定多様体の疎密と強い相関を持つ空間的に非一様な分布であることの数値的な証拠を紹介する。また、第二固有値に属する固有関数の非一様性に対する有限時間Lyapunov指数を用いた現象論的議論も報告する。
- 超一般化Boole変換における無限測度のエルゴード性の証明 / ○大久保 健一 (京大情報), 梅野 健 (京大情報) [概要]
講演者は超一般化Boole変換において, α=±1の時に, Lebesgue測度を保存し, 無限測度のエルゴード性が
成り立つことを証明する. これによって, 超一般化Boole変換はExact性を持つ領域, 無限測度のエルゴード性を持つ領域,
散逸領域の3つの領域を持つことが分かった.
- 決定論的拡散の一般化拡散係数のルベーグスペクトル分解 / ○梅野 健 (京都大学) [概要]
決定論的拡散の一般化拡散係数のルベーグスペクトル分解が得られたので、
決定論的拡散の一般化拡散係数の定義、
決定論的拡散の一般化拡散係数のルベーグスペクトルとの明示的な関係を与え、
オンサーガーの相反定理との関係について明らかにする。
▷ 離散システム(1) [3月5日:09:30-10:50:Room C (6310)]
- 有向距離空間上の最小ゼロ拡張問題 / ○水谷 隆平 (東京大学), 平井 広志 (東京大学) [概要]
最小ゼロ拡張問題とは,距離の定まった有限集合上に新たにいくつかの要素を配置するときに,すべての2要素の組についてのコストと距離の積の和の最小値を求める問題であり,最小カット問題,多分割カット問題などを含む問題である.この問題は多項式時間可解である場合とNP困難である場合があるが,それは有限集合上で定まっている距離に依存する.距離が対称である場合については,Hirai(2016), Karzanov(1998)により多項式時間可解かNP困難かのクラス分けが完了している.本発表では,距離が非対称(有向)である場合のクラス分けを紹介する.
- ハイパーグラフマッチングゲームの凸性 / ○隈部 壮 (東京大学), 前原 貴憲 (理研 AIP) [概要]
協力ゲーム理論とは、複数のプレイヤーが協力することによってより多くの利得が得られるような状況をモデル化したものである。プレイヤーの集合いくつかに対して、それぞれその全員が協力したときの利得の値を与えて定義されるゲームをハイパーグラフマッチングゲームと呼ぶ。本研究では、ハイパーグラフマッチングゲームが凸ゲームと呼ばれる良いクラスに属するための必要十分条件と、その多項式時間の判定アルゴリズムを与えた。また、凸ゲームになるケースに対して、シャープレイ値と呼ばれる、「良い」利益分配の方法を与える値を多項式時間で計算する方法を示した。さらに、同じケースに対して、対応する詰込型の線形計画問題の整数性を証明した。
- 頂点近傍重み付きシュタイナー木問題に対する近似アルゴリズムの設計 / ○馬原 凌河 (京都大学), 小林 佑輔 (京都大学) [概要]
最小コストシュタイナー木問題は最も古典的なNP困難な問題のひとつである.無向グラフと非負の辺コスト関数,そしてターミナルと呼ばれる頂点部分集合が与えられたとき,すべてのターミナルを連結にするような総コスト最小の部分グラフを見つける問題である.目的関数を変えることで,この問題の様々な変種を考えることができる.頂点周りの辺コストの最大値の各頂点における和を最小にする最小パワーシュタイナー木問題や,頂点に重みが付加した頂点重み付きシュタイナー木問題などが例として挙げられる.本講演では,これらを一般化した問題に対する近似アルゴリズムの設計を紹介する.
- 整数計画における遷移問題の計算量 / ○木村 慧 (埼玉大学), 鈴木 顕 (東北大学) [概要]
本講演では,各変数の取り得る値に上下界のある整数計画問題とその実行可能解が2つ与えられた際に,一方の解からもう一方へ,実行可能性を保ちながら段階的に変換することで遷移できるか否かを判定する問題を扱う.ここで,一度の変換においては,1つの変数への値の割当を変えることのみが許される.この種の問題は「遷移問題」と呼ばれ,組合せ最適化分野において近年盛んに研究が行われている問題である.この問題は一般の整数計画に対してはPSPACE完全となるため,本講演では,整数計画の部分クラスにおける計算複雑さを解析した.具体的には,整数計画問題における制約の符号情報のみから計算できる指標用い,その指標の値が1未満,ちょうど1,1より大きい場合にはそれぞれの遷移問題が定数時間可解,弱coNP完全かつ擬多項式時間可解,PSPACE完全であることを示した.これにより,特に,ホーン不等式系や二次不等式系における遷移問題がcoNPに属し,かつ擬多項式時間可解であることを明らかにした.
▷ 離散システム(2) [3月5日:11:00-12:20:Room C (6310)]
- 局在化された固有ベクトルをもつ内周の大きな正則エクスパンダーグラフ / ○佐竹 翔平 (神戸大学 大学院システム情報学研究科) [概要]
正則グラフGの隣接行列の固有ベクトルの「局在化」とGの内周との関係に関する研究は, Brooks-Lindenstrauss (2013)で提案された.
Ganguly-Srivastava (2018)は,固有ベクトルの局在化の条件のもとでの内周の上界式を証明し,その最良性を非明示的に示した.
その後,Alon-Ganguly-Srivastava (2019)は,すべての素数dに対して,Ganguly-Srivastava
(2018)の評価式の最良性を示す(d+1)-正則エクスパンダーグラフを明示的に構成した.
本講演では,Alon-Ganguly-Srivastava (2019)の構成を,一般の次数に拡張する.
- On p-frame potential of determinantal point processes on the sphere / ○平尾 将剛 (愛知県立大学情報科学部) [概要]
近年,確率点過程の中でも行列式点過程の応用研究に関心が高まっている.本講演では行列式点過程の中でもその典型例である球面アンサンブル,調和アンサンブル,およびジッタードサンプリグに着目し,そのランダム点配置が持つp-フレーム・ポテンシャルの期待値の評価を行う.さらにその応用の一つとして,球面上の一様分布から生成されるランダム点配置と比べ,これら行列式点過程の生成するランダム点配置がタイト・フレームを近似する良い点配置であることを示す.
- モンテカルロ法によるcubature公式の構成 / ○早川 知志 (東京大学) [概要]
確率分布上の数値積分法にはモンテカルロ積分や準モンテカルロ法 (QMC) などがあるが、被積分関数が多項式でよく近似できる場合には、cubatureという手法も用いられている。cubatureとは与えられたいくつかのテスト関数 (典型的には多項式) の積分値を与えるようなサンプル点の配置と重みからなる積分公式である。cubature公式の存在は一般にTchakaloffの定理により非構成的に保証されているが、その構成は領域・測度・テスト関数に良い性質がある具体的な場合に代数的・組合せ的な手法を用いて与えられることが多かった。今回は一般的な仮定の下で、cubature公式が確率1で構成できることを示し、そのアルゴリズムを解説する。またその仮定を満たさない場合にも我々の手法が有効であることをデータ圧縮の観点から説明する。
- quadrature公式の有理性について / ○澤 正憲 (神戸大学大学院システム情報学研究科), 内田 幸寛 (首都大学東京大学院理学研究科) [概要]
本講演では,まず整数論のWaring問題に端を発するある不定方程式の求解問題を紹介したのち,有理性をもつquadrature公式の存在問題,直交多項式の零点の有理性判定,Christoffel-Darboux核上の有理点の解析などとの関連性について概説する.そのうえで,内田幸寛氏(首都大東京)との共同研究で得られた,解の非存在定理,球面デザイン論への応用などについて研究成果を報告したい.
▷ 離散システム(3) [3月5日:13:30-14:50:Room C (6310)]
- 閉曲面の既約な4-連結三角形分割の生成とその応用 / ○篠木 寛鵬 (東京大学) [概要]
球面以外の閉曲面の4-連結三角形分割は三次元大域剛である,ということがConnelly(2014)によって予想され,現在も未解決である.この予想は,既約な4-連結三角形分割についてのある性質が示されれば解決される.本講演では,各閉曲面の既約な4-連結三角形分割が有限個であることを示し,それらを生成するアルゴリズムを提示する.さらに,計算機実験によって種数の小さな閉曲面について予想が成立することを示す.
- 3次元以下のgenericな群対称テンセグリティの普遍剛性の特徴づけ / ○大場 亮俊 (東京大学情報理工学系研究科数理情報学専攻) [概要]
無向グラフG=(V,E)とVのユークリッド空間への埋め込みpの組(G,p)をフレームワークと呼ぶ.フレームワーク(G,p)が普遍剛であるとは,対応する辺の長さが等しい任意の次元のフレームワーク(G,q)が(G,p)と合同変換で移り合うことをいう.
またフレームワークの各辺をバネに置き換えたときに力が釣り合うようなバネ定数の定め方を自己応力という.
Gortler and Thurston (2014)により,一般性の仮定の下,普遍剛性はラプラシアン行列が最大ランクかつ半正定値である自己応力の存在と同値であることが示された.
本研究ではこの結果を3次元以下の群対称なフレームワークに対して拡張した.また辺に伸び縮みを許すテンセグリティについても.拡張した.
- 擬似乱数Xorshift128+の非乱数性 / ○原本 博史 (愛媛大学), 松本 眞 (広島大学), 斉藤 睦夫 (広島大学) [概要]
2016年に提唱された擬似乱数生成法Xorshift128+は、スマートフォンなどの低コストな計算環境向けに設計されており、JavaScriptの標準擬似乱数として採用されている。この生成法は高速生成のために簡単な漸化式を基礎とし、様々な標準的な統計的検定に合格するようなパラメータによって特徴付けられる。最近、我々はXorshift128+の3つの連続する出力から定まる3次元立方体内のランダムポイントをプロットすることで、極めて簡単な平面構造があることを発見した。またその平面の方程式を、算術的和と排他的論理和の類似性に注目して導いた。この発表では、その証明の概略とシミュレーションに
与える影響を紹介する。
- AES暗号SubByte変換のサイクル分解が与える安全性への影響 / ○山本 ひなの (お茶の水女子大学大学院), 萩田 真理子 (お茶の水女子大学) [概要]
今日の共通鍵暗号方式の標準規格であるAES(Advanced Encryption Standard)と他の暗号の安全性を比較するための評価研究として,これまでに偏りのあるデータの集合を暗号化した際の暗号文の偏りを検出することで乱数性を評価してきた.偏りのあるデータとしては,入力値として0を極端に多くしたものを用いていた.
本研究では,AES暗号の変換の1つであるSubByte変換を置換としてサイクル分解して得られたサイクルに着目した偏りを持たせることで,上記の設定でAES暗号の乱数性の検定を行った場合よりも1つ上のラウンドまで棄却することに成功した.
この発表では,Sボックスのサイクルが暗号の安全性に与える影響について紹介する.
▷ 離散システム(4) [3月5日:15:00-16:20:Room C (6310)]
- パフィアンペアに対する一般化行列木定理 / ○大城 泰平 (東京大学) [概要]
グラフの全域木の数え上げで有名な行列木定理は,本質的には正則マトロイドの基を数え上げる定理である.Webb (2004) は,正則マトロイドの組であって,行列木定理を通して共通基の数え上げを行えるクラスとして,パフィアンペアの概念を導入した.本発表では,平面二部グラフの完全マッチングや有向全域木など,行列式計算による数え上げが可能ないくつかの離散構造がパフィアンペアであることを示す.また,各要素に重みがついているパフィアンペアに対し,最大重みの共通基の数を計算する強多項式時間アルゴリズムを提案する.
- マトロイドパリティ問題における数え上げ / ○的矢 知樹 [概要]
全域木の個数、有向全域木の個数はラプラシアン行列の行列式と等しく、解の個数を効率的に計算できることが知られている。これらはマトロイドの共通基の数え上げとして一般化されている。また、平面グラフに代表されるパフィアンなグラフ上の完全マッチングの個数はタット行列のパフィアンと等しいことが知られている。これらの問題の一般化としてパフィアンなマトロイドパリティ上のパリティ基の数え上げを導入し、点素路の数え上げに関するLGV
(Lindström–Gessel–Viennot)補題の一般化など幾つかの数え上げ可能な問題を新たに与える。また、最小重みパリティ基の個数は重み付きマトロイドパリティのアルゴリズムを用いることで多項式時間での計算が可能であることを示す。
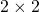 型分割行列のランクを求める組合せ的多項式時間アルゴリズム / 平井 広志 (東京大学), ○岩政 勇仁 (国立情報学研究所) [概要]
型分割行列のランクを求める組合せ的多項式時間アルゴリズム / 平井 広志 (東京大学), ○岩政 勇仁 (国立情報学研究所) [概要]
二部グラフの最大マッチング問題の代数的拡張である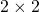 型分割行列のランクを求める問題に対して,増加路を用いた組合せ的な多項式時間アルゴリズムを与える.
型分割行列のランクを求める問題に対して,増加路を用いた組合せ的な多項式時間アルゴリズムを与える.
- 作用素スケーリングに対する情報幾何 / 松田 孟留 (東大・理研), ○相馬 輔 (東大) [概要]
作用素スケーリングは(Gurvits 2004)によって行列スケーリングの非可換版として導入された問題で,Edmonds問題やBrascamp-Lieb不等式への応用が近年見つかりつつある.元々,行列スケーリングは情報幾何との密接な繋がりがあり,例えば行列スケーリングの代表的なアルゴリズムであるSinkhorn反復は,Fisher計量に対する交互e射影に一致する.ところが,作用素スケーリングにおいて同様の情報幾何的な解釈ができるかは分かっていなかった.本研究では,作用素スケーリングの代表的アルゴリズムである作用素Sinkhorn反復が,量子情報幾何で知られているSLD計量に対する交互e射影に一致することを示す.
▷ 数理ファイナンス(1) [3月5日:11:00-12:20:Room D (6317)]
- 時間非一様なMarkov過程の効率的サンプルパス生成とバリア・オプションのGreeks計算 / ○石谷 謙介 (首都大学東京) [概要]
講演では,停止時刻を含むようなWiener汎関数に対する超関数微分の計算方法と,その応用としてバリア・オプションの1次オーダーのGreeksの準解析的計算方法を提案する.更に,この提案手法を用いてGreeksを計算するために必要となる,3次元Bessel橋やBrownian meanderといった時間非一様なMarkov過程の効率的サンプルパス生成方法についても紹介し,提案手法を用いてバリア・オプションのGreeksを高精度に計算できることを確認する.
- バリアーオプションのヘッジ公式について / ○今村 悠里 (金沢大学理工学域数物科学類) [概要]
本研究では,ノックアウトオプションおよびノックインオプションのヘッジポートフォリオを与える.確率過程がある領域を経由しないという条件を,一般化された鏡像原理によって, 到達場所の領域を反転させることで得られるヘッジ公式を提案する.また,バリアーオプションのヘッジ手法であるストライクスプレット法とカレンダー法との関連についても紹介する.
- 保型形式の確率論とその応用 / ○橋本 玲南 (立命館大学), 赤堀 次郎 (立命館大学) [概要]
本講演では保型形式を広い意味での双曲ラプラシアンの固有関数として理解し,その確率論的な意味を考え,その数値解析への応用をめざす.双曲ラプラシアンに関する数値解析は,確率volatility モデルを通じて,数理ファイナンスにおいても重要である.
- ディスカウントキャッシュフロー法で求めたCDSのColVA / ○山下 政紘 (法政大学理工学研究科), 安田 和弘 (法政大学) [概要]
本研究では, White[2018]で提案されているディスカウントキャッシュフロー法によるCDSのプライシングモデルを用いて, CDSの担保評価調整(ColVA)を求めた. また, 多変量ベルヌーイ分布による結合確率表現を用いることで, 取引当事者のデフォルトを考慮した. 本講演では, 求めたColVAの性質や他の信用評価調整であるCVAやDVAとの比較も行う.
▷ 数理ファイナンス(2) [3月5日:13:30-14:50:Room D (6317)]
- 結晶格子上のランダムウォークを用いた後退確率微分方程式の近似 / 関根 順 (大阪大学基礎工学研究科), 深澤 正彰 (大阪大学基礎工学研究科), 安藤 眞志 (大阪大学基礎工学部), ○田中 章博 (大阪大学基礎工学研究科/三井住友銀行) [概要]
デリバティブの評価において、XVAと呼ばれる評価調整を加味しプライシングすることが市場慣行になりつつあり、実務において段階的に対応が進められている。一方、XVAはBSDEの解を用いて定義されることから、数値計算が難しく、近似的な手法で計算されている。本研究では、結晶格子上のランダムウォークを用いたBSDEの近似について紹介する。
- A Discrete-Time Clark-Ocone Formula and its Applications / 赤堀 次郎 (立命館大学), ○大熊 香里 (株式会社QUICK) [概要]
Akahori-Amaba-Okuma (2018) の離散版のClark-Oconeを紹介し、今後の展開について概観する。
- 三項モデルにおけるDPを用いた期待効用とPFPPの期待効用の比較 / ○佐藤 大地 (法政大学 理工学研究科), 安田 和弘 (法政大学) [概要]
日本応用数理学会2019年度年会では二項モデル下で変化率が可予測過程に従う場合の動的計画法(DP)を導入し, Angoshtari et al. (2019)で考えられている可予測フォワードパフォーマンス過程(PFPP)との期待効用の比較を行った. この場合, DPはモデルリスクを含むことになるが, 時刻0で得られる期待効用はDPの方が高くなる結果であった. 本講演では三項モデルでのDPならびにPFPPでの期待効用等を近似的に導出し比較を行う.
- 条件付歪曲期待値の時間整合性:非均一な分散構造を持つモデルの解析 / ○関根 順 (大阪大学大学院基礎工学研究科), 山田 貴一 (大阪大学大学院基礎工学研究科) [概要]
Ma, Wong, and Zhang (2018; arXiv)で提案された時間整合性を持つ条件付き歪曲期待値の計算について以下の2点を中心に考察を行う
1)分散が非均一であるMarkov連鎖モデルの例:半3項モデルと2項モデル
2)適当にスケーリングし時間刻み幅を0に収束させる拡散極限と偏微分方程式の導出
▷ 数理ファイナンス(3) [3月5日:15:00-16:20:Room D (6317)]
- Queue-Reactive Hawkes 過程を用いた株式板情報と価格変動の関係の分析 / ○野原 眞 (三菱UFJトラスト投資工学研究所/一橋大学大学院経営管理研究科), 中川 秀敏 (一橋大学大学院経営管理研究科) [概要]
本研究では、Wu et al.(2019)が導入したQueue-Reactive Hawkes過程を用いて、本邦株式市場の板情報の注文タイプおよび注文数量と仲値の変化との関係について分析を行った。
主な結果として、仲値の上昇は最良気配値における待ち注文数量の厚みに大きく依存すること、仲値が上昇(下落)した後の最良売り(買い)気配値における待ち注文数量が極端に多くなければ、価格が上昇(下落)しやすいという価格のモメンタムが見られること、などが確認された。
- 機械学習による企業成長性の判別分析 / ○斉藤 美穂 (青山学院大学), 山中 卓 (武蔵野大学) [概要]
本発表では企業の成長性を予測する機械学習モデルの構築について報告する.本邦の中小企業データベースを用いて,過去の企業情報から将来の売上高増加の有無を判別する機械学習モデルを複数構築し,それらの判別結果を比較する.
- ユーザの位置情報を活用した、株価に影響する営業資産の最適な組み合わせ探索方法について / ○金子 拓也 (KDDI Research & ICU), 木村 塁 (KDDI Research & KDDI), 美嶋 勇太朗 (KDDI Research & KDDI) [概要]
本発表では、企業が保有する様々な営業用アセットの中で、株価の変化と最も相関するアセットの組み合わせを探索する方法を提案する。企業の多くは、業績の安定化を目的として複数事業から成るポートフォリオを構築している。株価とは将来に渡って支払われる配当金の期待利回りによる割引現在価値の総和であり、株価の変化は配当金の状況の変化、つまりは事業ポートフォリオの状態の変化がタイムリーに反映された結果もたらされるものと整理できる。そうなると投資家は、売買対象企業が保有するすべての事業用アセットの状況を把握して意思決定を行わなければならないが、現実的には複数の状況について逐次同期的に把握することは困難であろう。そこで部分的に注目しているものと想定すると、今度は企業経営者は、投資家が注目しているアセット群を株式価値最大化のために把握しておく必要がある。このような課題に取り組むとき、簡易に想起される技術的な問題として、営業用アセットのタイムリーな運用状況をどのように把握するのかということが考えられるが、これに対しては、ユーザの位置情報を活用する。また、複数のアセットの最適組み合わせの探索において、組み合わせ数が膨大となる問題に対してはGAで最適化を図ることを考える。発表では、探索の結果得られたアセット群の業績状況を利用した簡易な株式売買の実験結果も併せて紹介する。なお、本研究は特願2020-000405と特願2020-001705に基づく。
▷ 折紙工学(1) [3月5日:09:30-10:50:Room E (6318)]
- 一定厚のパネルで構成される二方向平坦折り可能な剛体折紙 / ○下田 悠太 (東京大学), 舘 知宏 (東京大学), 佐藤 淳 (東京大学) [概要]
剛体折紙を建築など大きい構造に応用するとき、パネルの厚みが問題となる。単一の厚みのパネルで折りたたみ可能な変形機構として、egg boxとその一般化を取り上げる。折りたたむために必要な拘束条件を明らかにして、その条件を満たす形状のバリエーションについて検討した。また、この構造を用いた仮設建築物のデザイン提案を行う。
- 複合材を用いた軽量折紙展開構造物 / 安藤 顕祐 (日建設計), 出水 文二 (日建設計), 重松 瑞樹 (日建設計), 玉井 宏樹 (日建設計), 松尾 淳 (帝人), 水田 悠生 (帝人), 宮田 武志 (GHクラフト), 定延 治朗, 須藤 海 (東京大学), ○舘 知宏 (東京大学) [概要]
繊維強化プラスチック(FRP)の複合材を用いた、軽量な展開構造物を提案する。剛性の高いCFRPのパネルの間に柔らかいマトリクス材のヒンジが埋め込まれた折り線レイアウトを平面状態において行うことによって、折り目のついたシート状のモジュールを一体成型した。多目的最適化による形状設計、座屈解析と展開機構解析、ファブリケーションプロセス、IASSでのパビリオン(片持ちキャノピー)展示について報告する。
- 菱形タイリングに基づく非周期タイリング機構 / ○割鞘 奏太 (東京大学), 野老 朝雄, 舘 知宏 (東京大学) [概要]
東京2020オリンピック・パラリンピックのエンブレムの白色部分を剛体、藍色の長方形部分を「隙間」とすることで、剛体の角でピン接続された1自由度の平面メカニズムを構築できることを示す。エンブレムが菱形の非周期的タイリングをベースとし、菱形の各辺の中点を取った長方形から構成されていることに起因する。ベースとなる菱形タイリングは任意にとることができるため、このメカニズムはReschのメカニズムの非周期タイルへの一般化になっている。
- 有限要素法を用いたたわみを考慮した三次元モデルによる日本古来の扇の視覚効果の検証 / ○山崎 桂子 (明治大学), 阿部 富士子 (明治大学), 萩原 一郎 (明治大学) [概要]
平安時代に生まれた日本の扇は,平面を放射状の蛇腹構造に折り上げ、骨を差しこみ、上下で円弧方向に収縮率の異なる構造となるよう作成されている。この構造のため、扇は平面では成し得ない視覚効果を持つ。この視覚効果を逆算的に考慮して扇面画は描かれていると考えられるが、貴重な文化財である扇に負荷を掛ける検証は難しい。デジタル空間で扇のモデルを作成し、扇のたわみを考慮した視覚効果の検証を行った。
▷ 折紙工学(2) [3月5日:11:00-12:20:Room E (6318)]
- 扇面図から扇絵を推測するための3次元コンピュータグラフィックス / ○佐々木 淑恵 (明治大学), 阿部 富士子 (明治大学), 山崎 桂子 (明治大学), 萩原 一郎 (明治大学) [概要]
扇は放射状に広がり,円弧方向では折り畳まれ,上下で収縮率の違う蛇腹構造を伴うために,折りによる凸凹が「扇絵」の見え方に影響を与える.「扇絵」は,扇の状態で美しく見えるように凸凹を構図に配慮しなければならない.デジタル空間の中で扇面図から扇を作成するアルゴリズムを考え,製作なしに扇絵の検証を行うことを目的とした.可視化した扇により形状を自由に動かし,画面上で様々な角度からの検討が可能になった.
- Ruling配置の推定による曲線折りを含む展開図の折りのシミュレーションとその結果の向上手法 / ○佐々木 好祐 (筑波大学), 遠藤 結城 (筑波大学), 金森 由博 (筑波大学), 三谷 純 (筑波大学) [概要]
展開図から折った後の形を生成する方法の1つにOrigami Simulatorを用いたシミュレーションがあるが,これは直線での折りにしか対応していない.本研究ではこのシミュレータを用いて曲線の折りを含む折り紙のシミュレートを近似的に実現することを目的とする.シミュレーション結果の向上のために取り組んでいる曲げエネルギーと曲面の法線を用いた最適化手法と,入力展開図の生成手法について説明する.
- 任意の多角形を一様縮小した形に剛体折りたたみ可能なスリット付き展開図生成手法 / ○山本 陽平 (筑波大学), 遠藤 結城 (筑波大学), 金森 由博 (筑波大学), 三谷 純 (筑波大学) [概要]
折り紙は,工学の分野において,収縮・展開が容易な構造物の設計に活用できることが知られている.折りのパターンが豊富であれば,新たな構造物の作成が期待できる.本研究では,与えられた多角形と相似で、縮小した形に折りたためる折りのパターンに着目する.既存のパターンの一部に切れ込みを入れ,山谷の割り当てを変えることで,縮小した形に折りたためる剛体折りのパターンを新たに提案し,厚みのある素材で作成しため報告する.
- 三角形ねじり折りの連結による展開図生成とその剛体折り可否判定 / ○海野 真誼 (筑波大学), 遠藤 結城 (筑波大学), 金森 由博 (筑波大学), 三谷 純 (筑波大学) [概要]
三角形のねじり折りが4つ連結してできる容易に展開収縮可能な展開図がある。しかし、この三角形のねじり折りは剛体折り不可能なため、展開図全体も剛体折りできない。そこで折り線の長さと角度を変数として剛体折り可能な三角形のねじり折り4つを連結させ、展開図全体を剛体折り可能にする解が存在するか探索を行った。本手法では3つまで連結した展開図が剛体折り可能であることを確認した。しかし、4つを連結することが可能な解は存在しないという結論を得た。
▷ 折紙工学(3) [3月5日:13:30-14:50:Room E (6318)]
- 有限要素法を用いたダイヤモンドシェルの折紙工学からのアプローチ / 阿部 綾 (明治大学), ○崎谷 明恵 (明治大学), 萩原 一郎 (明治大学) [概要]
吉村パターンから着想を得て三浦公亮氏によってダイヤモンドシェル構造は生まれた。本研究は、この構造に注目し円筒型薄肉構造を研究することにより、これからの新しい構造に生かすことを目的とする。まずは有限要素法を用いたシミュレーションソフトウェアでダイヤモンドシェル構造を計算し、検討を試みる。
- 双安定性を持つ折り畳み構造を利用した防振機構の設計と性能評価 / ○山口 航矢 (明治大学理工学部機械工学科), 石田 祥子 (明治大学理工学部機械工学科) [概要]
立体状態と完全に折り畳まれた状態で安定となる双安定性を持つ折り畳み構造に、線形ばねを付加すると、非線形ばね特性を得ることができ、それを利用した防振機構がある。本研究では、以上のような防振機構を2種類設計し、それらの防振性能を比較した。その結果、ばね機構の設計が共振周波数や高周波域での振動に影響を及ぼすことを報告する。
- 有限要素法による遮音特性シミュレーション技術の開発と折紙コアへの応用 / ○阿部 綾 (明治大学), 屋代 春樹 (明治大学), 萩原 一郎 (明治大学) [概要]
従来の遮音特性評価法には有限要素法で任意位置での音圧値を容易に求められる利点を活かし,定義に従って全ての節点での音圧から音響エネルギー密度を求め透過損失を算出することがあるが,これに対し,透過損失の算出に実験との対比をより容易とする効果的な代表節点の位置を絞り込む手法が提案されている.しかし,これには理論値と計算値に誤差が生じる問題が残されており,本報ではこの問題を解決する手法について論じ折紙コアへの適用を図る.
- 折紙工学援用による自動車クラッシュボックスの圧潰エネルギー吸収特性向上 / ○楊 陽 (明治大学), 萩原 一郎 (明治大学) [概要]
乗員の安全保護のため、車両前部の左右に配置されるクラッシュボックスにできるだけ多く圧潰エネルギーを吸収させることは非常に重要である。折紙工学の研究成果から側面壁に適当に折り線を入れることによって圧潰長さは構造全長の90%以上続けられる特性を得ているので、一般的な横断面構成、軸方向の段差付きの新型クラッシュボックスの開発を図る。クラッシュボックス構造を分析し、パラメータ変化により吸収エネルギー最大を目的とする解析について検討を行う。
▷ 折紙工学(4)(〜16:40) [3月5日:15:00-16:40:Room E (6318)]
- ハニカム状トラスコアパネルの衝撃エネルギ吸収特性評価 / ○浅上 隆登 (明治大学理工学部機械工学科), 石田 祥子 (明治大学理工学部機械工学科) [概要]
自動車の衝撃試験において、衝突エネルギ吸収の性能要件を満たす軽量構造の開発が近年進んでいる。本研究ではトラスコアパネルにハニカム構造を取り入れたハニカム状トラスコアパネルを取り扱い、落錘による動的数値解析からエネルギの吸収の原理と座屈の形状、設計変数との関係を明らかにすることが目的である。
- 折り畳み構造のインバーション変形によるエネルギ吸収材の設計と評価 / ○伊藤 大悟 (明治大学大学院), 石田 祥子 (明治大学) [概要]
本研究の目的は,インバーション変形と呼ばれる優れたエネルギ吸収特性をもつ塑性変形を安定に生じさせることのできる折り畳み構造を設計し,性能を評価することである.設計変数が異なる構造を設計し,圧縮試験機を用いた静的な圧縮試験を行った結果とシミュレーションによる圧潰の結果を報告する.
- ビーズ正八面体上の閉測地線 / ○中島 香歩 (龍谷大学理工学部), 山岸 義和 (龍谷大学理工学部) [概要]
ビーズ正八面体上のビーズ測地線は、正八面体の表面を小さな正三角形に分割して得られるグラフ上の zigzag や、正八面体上の閉測地線との自然な対応をもち、その傾きは既約分数 p/q で表される。閉測地線は回転対称性をもち、その回転軸が正八面体の頂点を通るか面の重心を通るかは p,q に依存する。このことを、回転群のケイリーグラフが3部グラフであることを利用して示す。
- 三角形二面体の最小跡と等角共役点 / ○北原 百華 (龍谷大学理工学部), 山岸 義和 (龍谷大学理工学部) [概要]
三角形二面体の source unfolding は六角形または四角形となる。三角形上の点Pの等角共役点Qが、三角形二面体の最小跡の頂点として自然に現れる。Q が P の最遠点となるのは、P が外心のときで、そのとき三角形の三つの頂点も P の最遠点であり、Q は垂心となる。長方形二面体の source unfolding は、平面の長方形タイル張りのボロノイ領域として作られ、これも六角形または四角形となる。
- 昆虫の翅の折り畳みの幾何学と展開構造への応用 / ○斉藤 一哉 (九州大学大学院芸術工学研究院) [概要]
構造をコンパクトに折り畳む技術は様々なスケール,用途において必要とされる.昆虫たちは翅を獲得した3億年前から同じ問題に取り組み続けており,様々な興味深い解を見つけている.本講演では様々な昆虫の種の翅の折り畳み方式と,人工の展開構造物への応用について解説する.
▷ 数理医学 [3月5日:11:00-12:20:Room F (6325)]
- 開放進化系における要素の性質と頑健性 / ○小串 典子 (京都大学) [概要]
社会コミュニティや生態系や生物システムといった現実の大規模複雑系は、常に新規要素の系への参入と既存要素の絶滅の影響に晒されている。こうした複雑な系の挙動を個々の構成要素が従う規 則に立ち返り理解するため、系を重み付き有向ネットワークとして記述するグラフモデルを採用する。本公演では個々の要素が持つ性質が系の頑健性に与える影響について報告する。
- 複数の変数で表現される変量について、2時点における変量の値と各変数の値を観測したとき、変量の2時点の観測値の差に対する各変数の寄与を公平に推定する一つの統一的な方法について / ○村山 令二 (健康保険組合連合会) [概要]
実務では、例えば、6変数で表現される変量F(x,y,p,q,u,v)=xpu+yqv について、6変数が時間の関数で、2時点T0,T1における変量の値と6変数の値を観測したとき、2時点における変量の観測値の差に対する各6変数の寄与を、変量の表現式を線形近似せず、公平に推定する。1つの統一的な推定方法として、各変数を未知関数とするある連立常微分方程式の逆問題の解が用いられる。
- [40分講演] メンデルランダム化解析による因果関係の推定とゲノムワイド関連解析の重要性 / ○下川 和郎 (大阪大学), 成田 暁 (東北大学), 田中 博 (東北大学), 鈴木 貴 (大阪大学) [概要]
ゲノムワイド関連解析の成果が蓄積されてきた結果、これまで困難だったメンデルランダム化解析が可能になってきている。
しかしながらこの解析は多くの分野を跨ぐことになるため結果の信頼性を検証するのに多くの困難が想定される。
本講演では想定される問題点を一歩づつ検証してゆくことによって本解析法の重要性を議論する。
▷ 数理設計(1) [3月5日:13:30-14:50:Room F (6325)]
- 形状観測データに基づく舌の筋活動同定に関する研究 / ○小野 慎二郎 (名古屋大学情報学研究科), 畔上 秀幸 (名古屋大学情報学研究科), 竹内 謙善 (香川大学創造工学部), 道脇 幸博 (武蔵野赤十字病院), 菊地 貴博 (武蔵野赤十字病院) [概要]
食物を口から胃に送り込むまでの一連の動作は嚥下と呼ばれる.本研究では,被験者のCT画像やVF画像を基にして作成された舌の形状変動を用いて,舌の筋収縮を同定する問題を考える.筋収縮は収縮応力の発生としてモデル化され,超弾性体の強制変形問題として舌の運動が記述される.同定問題は,筋収縮活動率を変数として,強制変位に対する反力の2乗ノルムを最小化する問題として定式化される.本発表では,数値例も紹介する.
- スカラー波動方程式のソース項同定問題に対するH1勾配法 / ○辻村 賢祐 (愛知県立大学情報科学部), 代田 健二 (愛知県立大学情報科学部) [概要]
本研究では,スカラー波動方程式のソース項同定問題に対する数値的に安定な解法を考察する.本発表で対象とするのは,ソース項が変数分離形となっているスカラー波動方程式であり,時間にのみ依存する関数は既知とし,空間にのみ依存する関数を内部観測から同定する問題を考える.内部観測データを用いた汎関数を導入し,H1勾配法を適用することで数値アルゴリズムを構成する.数値実験により,その有効性を検証する.
- 消化管の蠕動運動を励起する筋配置同定問題 / ○齋藤 元滋 (名古屋大学), 佐原 資謹 (岩手医科大学), 畔上 秀幸 (名古屋大学) [概要]
消化管を模した平滑筋で構成された生体器官を超弾性体でモデル化し,消化管の蠕動運動を励起するような内部の筋活動を同定する問題を定式化し, その数値解法を示す.さらに,数値例を示し,解剖学による結果と比較する.
- On the existence of a solution to a shape optimization problem / ○畔上 秀幸 (名古屋大学), Julius Fergy T. Rabago (名古屋大学), 相野 眞行 (名古屋大学) [概要]
In this talk, conditions for the existence of a solution to a PDE-constrained shape optimization problem are discussed. Because such problems deal with shapes of domains, the convergence of sets is defined through convergence of functions that describe the boundary of the domains. Accordingly, the existence of optimal shape solution is proved by endowing the graph induced by the mapping from domain to state (and adjoint state) variable with a topology that has good compactness properties and showing that the shape functional associated with the optimization problem is (at least) lower semi-continuous. The former requirement is established through the continuous dependence of the state (and adjoint state) on the admissible design variable; that is, with respect to domain variations.
▷ 数理設計(2) [3月5日:15:00-16:20:Room F (6325)]
- 形状変化に基づく特発性側彎症患者別骨量変化の同定 / ○西川 弘一郎 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
医用画像データから有限要素モデルを構築するソフトウェアを用いれば,特発性側彎症患者の脊柱モデルを得ることができる.さらに,3次元形状編集ソフトウェアを用いれば,患者脊柱モデルを正常な形状に変形させることができる.本研究では,このようにして求めた変形を骨量の増減に置き換える問題を定式化して,その解法を示し,数値解を紹介する.その結果から,成因に関して考察する.
- 制約重量内の, 最適質量分布を求める 離散変分不等式とその解の収束 / ○海津 聰 [概要]
空間 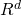 内の有界領域
内の有界領域 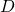 上で制約以下の重量をもつ
密度分布
上で制約以下の重量をもつ
密度分布 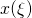 のなす最小(適)仕事量を与える最適密度の,
存在が保証されている.
そこでこの最適密度を与える離散スキームを, 陽的時間発展
離散スキームとして与え, 離散解の収束について考える.
その際, クーラント・ヒルベルト, 1937, にあるフリードリクス型
の不等式にヒントを得た, 新たな「
フリードリクス型の不等式」を与えて, これを用いて離散解の
収束を示したい.
のなす最小(適)仕事量を与える最適密度の,
存在が保証されている.
そこでこの最適密度を与える離散スキームを, 陽的時間発展
離散スキームとして与え, 離散解の収束について考える.
その際, クーラント・ヒルベルト, 1937, にあるフリードリクス型
の不等式にヒントを得た, 新たな「
フリードリクス型の不等式」を与えて, これを用いて離散解の
収束を示したい.
- 魚型超弾性体の泳ぎモード創生問題 / ○林 拓也 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]
魚を模した弾性体に周期的な物体力を負荷したときに発生する運動を理想的な泳ぎ運動に近づける形状最適化問題は,これまで線形弾性体を用いて定式化されてきた.本研究では,魚を超弾性体と仮定して,泳ぎ運動を有限変形によってモデル化する.
- 3次元有限要素流れ解析におけるPOD法の適用について / ○松本 純一 (国立研究開発法人 産業技術総合研究所) [概要]
随伴法や感度解析法を用いた逆問題への適用が可能な3次元有限要素流れ解析におけるPOD法について考察する。3次元有限要素流れ解析には、複雑形状に優れた四面体要素による直交基底気泡関数要素安定化法を採用し、分散メモリ並列計算を導入したPOD法の適用について説明する。
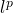 ソボレフ不等式の最良定数 / ○山岸 弘幸 (都立高専) [概要]
ソボレフ不等式の最良定数 / ○山岸 弘幸 (都立高専) [概要]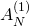 型ミューテーションの線形化 / ○野邊 厚 (千葉大学), 松木平 淳太 (龍谷大学) [概要]
型ミューテーションの線形化 / ○野邊 厚 (千葉大学), 松木平 淳太 (龍谷大学) [概要]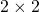 型分割行列のランクを求める組合せ的多項式時間アルゴリズム / 平井 広志 (東京大学), ○岩政 勇仁 (国立情報学研究所) [概要]
型分割行列のランクを求める組合せ的多項式時間アルゴリズム / 平井 広志 (東京大学), ○岩政 勇仁 (国立情報学研究所) [概要]